Comentario Final

Creo que la bitácora nos ayudaba a saber que era lo que aprendíamos y así poder repasarlo. E incluso entenderlo mejor al momento de buscar información en la Web. Definitivamente es de gran apoyo, aunque muchos se daban a la tarea de comentar que no nos serviría de nada. Todos debíamos hacerlo pues era una manera relativamente sencilla de ganar los puntos. Gracias al catedrático por impartir su clase. 

Diferencia Simétrica

En teoría de conjuntos, la diferencia simétrica de dos conjuntos es una operación que resulta en otro conjunto cuyos elementos son aquellos que pertenecen a alguno de los conjuntos iniciales, sin pertenecer a ambos a la vez. Por ejemplo, la diferencia simétrica del conjunto de los números pares P y el conjunto de los cuadrados perfectos C es un conjunto D que contiene los cuadrados impares y los pares no cuadrados:

${\displaystyle C=\{1,4,9,16,25,\ldots \}}$

${\displaystyle D=\{1,2,6,8,9,10,12,14,18,\ldots \}}$

La diferencia simétrica de conjuntos se denota por Δ, por lo que P Δ C = D.

Diferencia de Conjuntos

En teoría de conjuntos, la diferencia entre dos conjuntos es una operación que resulta en otro conjunto, cuyos elementos son todos aquellos en el primero de los conjuntos iniciales que no estén en el segundo. Por ejemplo, la diferencia entre el conjunto de los números naturales N y el conjunto de los números pares P es el conjunto de los números que no son pares, es decir, los impares I:

${\displaystyle P=\{2,4,6,8,10,12\ldots \}}$

${\displaystyle I=\{1,3,5,7,9,11\ldots \}}$

Como no hay ningún número par que no sea un número natural, la diferencia P menos N no tiene ningún elemento, por lo que es el conjunto vacío. La diferencia entre dos conjuntos A y B se denota por A \ B ó A − B, por lo que: N \ P = I, y también P − N = ∅.

Unión de Conjuntos

En la teoría de conjuntos, la unión de dos (o más) conjuntos es una operación que resulta en otro conjunto, cuyos elementosson los elementos de los conjuntos iniciales. Por ejemplo, el conjunto de los números naturales es la unión del conjunto de los números pares positivos P y el conjunto de los números impares positivos I:

${\displaystyle I=\{1,3,5,\ldots \}}$

${\displaystyle \mathbb {N} =\{1,2,3,4,\ldots \}}$

La unión de conjuntos se denota por el símbolo ∪, de modo que por ejemplo, N = P ∪ I.

Intersección de Conjuntos

En teoría de conjuntos, la intersección de dos (o más) conjuntos es una operación que resulta en otro conjunto que contiene los elementos comunes a los conjuntos de partida. Por ejemplo, dado el conjunto de los números pares P y el conjunto de los cuadrados C de números naturales, su intersección es el conjunto de los cuadrados pares D 

P: (2,4,6,8,10)

C: (1,4,9,16,25)

D: (4,16,32,64)

{\displaystyle P=\{2,4,6,8,10,\ldots \}}

{\displaystyle C=\{1,4,9,16,25,\ldots \}}

{\displaystyle D=\{4,16,32,64,\ldots \}}

En otras palabras: Así, por ejemplo, si A = { a, b, c, d, e} y B = { a, e, i, o}, entonces la intersección de dichos conjuntos estará formada por todos los elementos que estén a la vez en los dos conjuntos, esto es: A B = { a, e}

La intersección de conjuntos se denota por el símbolo ∩ por lo que D = P ∩ C.

Conjunto

En matemáticas, un conjunto es una colección de elementos considerada en sí misma como un objeto. Los elementos de un conjunto, pueden ser las siguientes: personas, números, colores, letras, figuras, etc. Se dice que un elemento (o miembro) pertenece al conjunto si está definido como incluido de algún modo dentro de él.

Ejemplo: el conjunto de los colores del arcoíris es:

• AI = {Rojo, Naranja, Amarillo, Verde, Azul, Añil, Violeta}

Un conjunto suele definirse mediante una propiedad que todos sus elementos poseen. Por ejemplo, para los números naturales, si se considera la propiedad de ser un número primo, el conjunto de los números primos es:

• P = {2, 3, 5, 7, 11, 13, ...}

A Pensar

Estos son ejercicios asignados por el catedrático al final de la clase para hacer que nuestros cerebros trabajen, algunas veces son ejercicios con sumas, otras sobre contar cuantas figuras hay en una imagen o incluso los tan famosos “sudoku”. Cualquiera que sea, son divertidos de resolver cuando se cuenta con el tiempo debido. 

Clase Regular

Como cualquier clase, hemos aprendido y hecho ejercicios acerca de las tablas de verdad. Hemos utilizado muchos ejercicios del libro de trabajo, y realizamos un laboratorio en grupos de tres integrantes. En el cual resolvíamos problemas de disyunción y conjunción. Pero por un momento confundimos las fórmulas que existen para evaluar las proposiciones. 

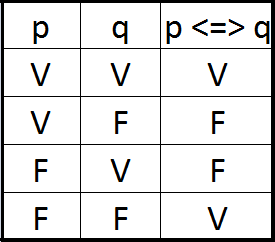
Bicondicional

En matemáticas y lógica, un bicondicional, (también llamado equivalencia o doble implicación, en ocasiones abreviado en español como ssi), es una proposición de la forma «P si y solo si Q» y se admite el bicondicional es verdadero en el caso de que ambos componentes tengan el mismo valor vertitativo. En otras palabras, que si P ocurre entonces también ocurre Q; y viceversa: si Q ocurre entonces también ocurre P.

Otra forma de expresar el bicondicional es decir que Q es una condición necesaria y suficiente para P. También se conoce con el nombre de complicación.

Negación de una Proposición

En lógica y matemática, la negación, también llamada complemento lógico, es una operación sobre proposiciones, valores de verdad, o en general, valores semánticos. Intuitivamente, la negación de una proposición es verdadera cuando dicha proposición es falsa, y viceversa. En lógica clásica la negación está normalmente identificada con la función que cambia su valor de verdadero a falso y viceversa. En Lógica intuicionista, de acuerdo a la interpretación de Brouwer–Heyting–Kolmogorov, la negación de una proposición p es la proposición cuyas pruebas son las refutaciones de p. 

Condicional Lógica

El condicional material, también conocido como implicación material, condicional funcional de verdad o simplemente condicional, es una constante lógica que conecta dos proposiciones. El condicional material intenta ser la versión formal del condicional en el lenguaje natural, el cual se expresa por medio de palabras como las siguientes:

·         Si llueve, entonces voy al cine.

·         Voy al cine si llueve.

·         Cuando llueve, voy al cine.

Simbólicamente, el condicional material se suele denotar de varias maneras. En orden descendente de frecuencia:

{\displaystyle A\to B}

{\displaystyle A\supset B}

{\displaystyle A\Rightarrow B}

Donde A y B son proposiciones cualesquiera. Las variables A y B se conocen respectivamente como el antecedente y el consecuente del condicional.

En lógica proposicional, el condicional material es una función de verdad binaria, que devuelve falso cuando A es verdadera y B es falsa, y devuelve verdadero en cualquier otro caso. En lógica de predicados, puede ser visto como una relación de subconjunto entre la extensión de predicados (posiblemente complejos).

Conjunción

En razonamiento formal, una conjunción lógica ( ${\displaystyle \land }$  ) entre dos proposiciones es un conector lógico cuyo valor de la verdad resulta en cierto sólo si ambas proposiciones son ciertas, y en falso de cualquier otra forma. Existen diferentes contextos donde se utiliza la conjunción lógica.

En lenguajes formales, la palabra "y" se utiliza en español para simbolizar una conjunción lógica. La noción equivalente en la teoría de conjuntos es la intersección ( ${\displaystyle \cap }$  ). En álgebra Booleana, la conjunción como operador binario entre dos variables se representa con el símbolo de punto medio ( · ).

En electrónica, una puerta AND es una puerta lógica que implementa la conjunción lógica.